Determining the line profile for a point source is fundamental for the analysis of spectrometer data and often the LSF can be described by a symmetric function. However, the line profiles from the CXO gratings are not symmetric and thus cannot, in general, be well described by a symmetric function such as a Gaussian. However, a Gaussian can describe the gross properties of the LSF, such as the width, and deviations from a Gaussian indicate how well a Gaussian can mimic the LSF. The Gaussian is symmetric about the mean, so the first deviation is asymmetry. Skewness is defined such that if more datapoints lie below the mean of the dataset it is known as negatively skewed. If the distribution is depleted of values below the mean it is positively skewed.
The second deviation from symmetry is known as kurtosis and compares the population of the tails of the dataset to that of the central region. If a distribution is more peaked than a Gaussian and/or the tails are more populated than a Gaussian then it has a positive kurtosis. If a distribution has tails less populated and/or is less peaked than a Gaussian then it has a negative kurtosis.
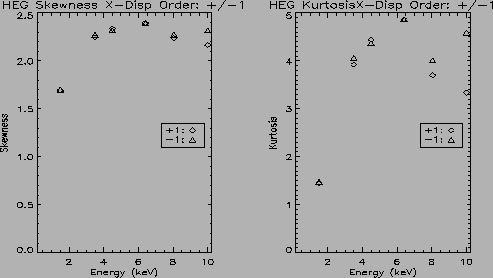
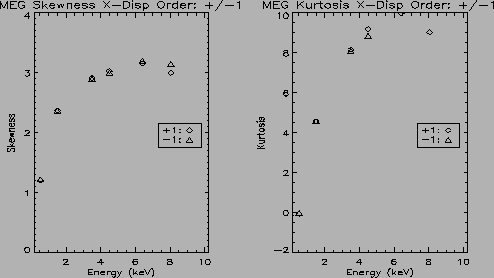
The skewness and kurtosis for the HEG and MEG data are shown in figure
3 for the dispersion direction. Similarly the
skewness and kurtosis for the cross-dispersion direction is shown in
figure 4. The skewness for the MEG and HEG data
area always positive indicating that there is more power above the
mean (at higher dispersion distance) when compared to a Gaussian. The
HEG skewness for the dispersion direction is fairly constant rising
slightly with energy from about 2.3 at 1.49 keV to 
2.5 at 10 keV
while that for the cross-dispersion direction range is from 1.7 up to
almost 2.5. The MEG skewness ranges from 2.4 to 3.5 for the dispersion
direction and from 1.2 to a value of 3.2 for the cross-dispersion
direction. The kurtosis for the HEG ranges from about 4.2 at 1.49 keV
to 6 at 10 keV for the dispersion direction and about 1.5 at 1.4 keV
and peaks near 5 at 6.4 keV for the cross-dispersion data. The
kurtosis for the MEG dispersion direction data ranges from 5 to
13 and for the cross-dispersion data ranges from zero at 1.4 keV and
increases to a maximum of 10 at 6.4 keV. This indicates that the LSF
has more power in the wings of the distribution than can be
accounted for with a Gaussian model. The skewness and kurtosis for
the plus and minus orders at 8 and 10 keV do not agree and this is
caused by the low number of simulated photons at these energies. One
reason that the MEG cross dispersion skewness is larger than that for
the HEG is the presence of the mis-aligned MEG gratings (see HETG
Ground Calibration: version 2.0 §6.4 Mis-Aligned Gratings).
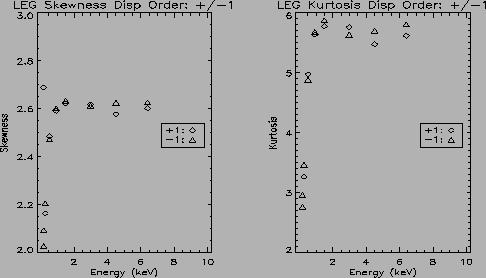
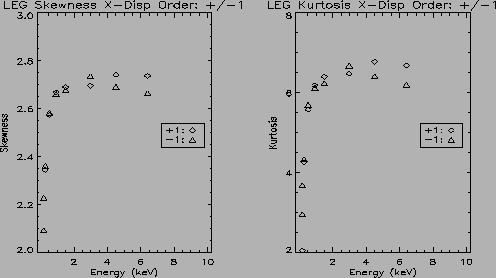
The skewness for the LETG LSF ranges from low of 2 up to 2.6 for
the dispersion direction and from 2 to 2.7 for the cross
dispersion direction. The kurtosis for the dispersion direction ranges
from 2 to just below 6 and from 2 to just above 6 in the cross
dispersion direction. So like the HEG and MEG LSF's the LEG LSF also
deviates significantly from a Gaussian.
In summary, Gaussian fits to the grating LSF is an inadequate description for sources with significant counts in a line. The kurtosis plots above show that the LSF is too much power in the peak and/or too much power in the wings to be fit with a Gaussian. The large values of the kurtosis indicate that fitting the LSF with symmetric functions may only be a first approximation since there are large deviations from symmetry.
However, more detailed modeling with MARX (eg. by including aspect blur) may reduce these effects and will be explored more fully in a future memo. In the next section we will compare the RMF's generated with the Gaussian approximation the simulated LSF's and later to flight data.
|
|
